| Отрезком [a,b] называется множество точек x, удовлетворяющих неравенствам: a ≤ x ≤ b при условии, что a < b
Интервалом (a,b) называется множество точек x, удовлетворяющих неравенствам: a < x < b при условии, что a < b Система отрезков [a1,b1],[a2,b2],...,[an,bn],... (до бесконечности) называется вложенной, если для любого натурального числа i верны неравенства: ai ≤ ai+1, bi ≥ bi+1 Аналогично определение вложенной системы интервалов. Задачи 1) У вложенной системы отрезков всегда ai < bj (при любых натуральных i и j). Доказать. 2) Теорема: вложенная система отрезков всегда имеет хотя бы одну точку, принадлежащую всем отрезкам системы (общую точку системы). Доказать. 3) Покажите, что вложенная система интервалов не всегда имеет общую точку. |
| Number of photos 2 | Photo gallery size 18 679 |
Go to photo gallery
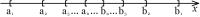 
|
|
| Descendants | Fans | Atheists |
|
|
|
|
| 3 | 0 | 0 |
| Go to the AI section of this object |
|
|
| Found 0 similarities |
|
Confirm that you are a human
|
|
| Expand | IMAGE SEARCH AI | Close | ||
|
|
||||
| Close | |||
|
|
|||
|
0 from 200 |
|
|
Last modified date:
|
|
| Cancel | |
| Cancel | |